Home » HHKG » Xác định giao tuyến giữa hai mặt phẳng
Xác định giao tuyến giữa hai mặt phẳng
March 29, 2012 | Posted by
Hồng Phi |
10
comments
Nếu máy tính bạn chưa cài đặt chương trình Java thì mô hình Geometer's Sketchpad có trong bài viết này không hiển thị được. Vì thế bạn vui lòng tải về và cài đặt Java tại địa chỉ http://java.com nhé!
Có 2 phương pháp xác định giao tuyến giữa hai mặt phẳng.
Phương pháp 1. Tìm 2 điểm chung phân biệt giữa hai mặt phẳng. Đường thẳng nối 2 điểm chung đó chính là giao tuyến của hai mặt phẳng.
Phương pháp 2. Tìm một điểm chung và phương của giao tuyến. (Để xác định phương của giao tuyến ta thường dựa vào quan hệ song song).
(Thông thường ta tìm mặt phẳng thứ ba chứa lần lượt 2 đường thẳng của 2 mặt phẳng cần xác định giao tuyến, nếu 2 đường thẳng này cắt nhau thì giao điểm chính là điểm chung của hai mặt phẳng, nếu 2 đường thẳng này song song sẽ cho ta phương của giao tuyến.)
Hệ quả. Nếu hai mặt phẳng cắt nhau lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng song song với hai đường thẳng đó (hoặc trùng với một trong hai đường thẳng đó).
Định lý. Nếu đường thẳng $a$ song song với mặt phẳng $(\alpha)$ thì mọi mặt phẳng $(\beta)$ chứa $a$ mà cắt $(\alpha)$ thì cắt theo giao tuyến song song với $a$.
Hệ quả. Nếu hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó.
Ví dụ 1. Cho hình chóp $S.ABCD$ có đáy là tứ giác có hai cặp cạnh đối không song song. Xác định giao tuyến giữa các cặp mặt phẳng $(SAC)$ và $(SBD)$; $(SAB)$ và $(SCD)$; $(SAD)$ và $(SBC)?$
Ví dụ 2. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Tìm giao tuyến giữa hai mặt phẳng $(SAB)$ và $(SCD)?$
Ví dụ 3. Cho hình chóp $S.ABCD$ và $E$ là một điểm trên cạnh $SC$. Tìm giao tuyến giữa hai mặt phẳng $(SAE)$ và $(SBD)?$
Bài 2. Cho tứ diện $ABCD$. Gọi $I, J$ lần lượt là trung điểm của $AC$ và $BC$ và $K$ là một điểm trên cạnh $BD$ sao cho $KD< KB$. Tìm giao tuyến của mặt phẳng $(IJK)$ với $(ACD)$ và $(ABD)$.
Bài 3. Cho tứ diện $ABCD$. Gọi $I, J$ lần lượt là trung điểm của $AD$ và $BC$.
a) Tìm giao tuyến của hai mặt phẳng $(IBC)$ và $(JAD)$.
b) Gọi $M$ là một điểm trên cạnh $AB$, $N$ là một điểm trên cạnh $AC$. Tìm giao tuyến của hai mặt phẳng $(IBC)$ và $(DMN)$.
Bài 4. Cho tứ diện $ABCD$ và $M$ là một điểm bên trong tam giác $ABD$, $N$ là một điểm bên trong tam giác $ACD$. Tìm giao tuyến của các cặp mặt phẳng $(AMN)$ và $(BCD)$; $(DMN)$ và $(ABC)$.
Phương pháp 1. Tìm 2 điểm chung phân biệt giữa hai mặt phẳng. Đường thẳng nối 2 điểm chung đó chính là giao tuyến của hai mặt phẳng.
Phương pháp 2. Tìm một điểm chung và phương của giao tuyến. (Để xác định phương của giao tuyến ta thường dựa vào quan hệ song song).
 |
| Giao tuyến của hai mặt phẳng đi qua hai đường thẳng song song. |
(Thông thường ta tìm mặt phẳng thứ ba chứa lần lượt 2 đường thẳng của 2 mặt phẳng cần xác định giao tuyến, nếu 2 đường thẳng này cắt nhau thì giao điểm chính là điểm chung của hai mặt phẳng, nếu 2 đường thẳng này song song sẽ cho ta phương của giao tuyến.)
Một số định lý thường dùng trong phương pháp 2.
Định lý. Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc dồng quy hoặc đôi một song song.Hệ quả. Nếu hai mặt phẳng cắt nhau lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng song song với hai đường thẳng đó (hoặc trùng với một trong hai đường thẳng đó).
Định lý. Nếu đường thẳng $a$ song song với mặt phẳng $(\alpha)$ thì mọi mặt phẳng $(\beta)$ chứa $a$ mà cắt $(\alpha)$ thì cắt theo giao tuyến song song với $a$.
Hệ quả. Nếu hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó.
Ví dụ 1. Cho hình chóp $S.ABCD$ có đáy là tứ giác có hai cặp cạnh đối không song song. Xác định giao tuyến giữa các cặp mặt phẳng $(SAC)$ và $(SBD)$; $(SAB)$ và $(SCD)$; $(SAD)$ và $(SBC)?$
Lời giải.
+) Tìm giao tuyến giữa $(SAC)$ và $(SBD)$.
Trong mặt phẳng $(ABCD)$, gọi $O=AC\cap BD$. Khi đó $$\left. \begin{array}{l} O\in AC\subset (SAC)\\ O\in BD\subset (SBD)\end{array}\right\} \Rightarrow O\in (SAC)\cap (SBD).$$Mặt khác $S\in (SAC)\cap (SBD)$. Vậy $(SAC)\cap (SBD)=SO$.
+) Tìm giao tuyến giữa $(SAC)$ và $(SBD)$.
Trong mặt phẳng $(ABCD)$, gọi $O=AC\cap BD$. Khi đó $$\left. \begin{array}{l} O\in AC\subset (SAC)\\ O\in BD\subset (SBD)\end{array}\right\} \Rightarrow O\in (SAC)\cap (SBD).$$Mặt khác $S\in (SAC)\cap (SBD)$. Vậy $(SAC)\cap (SBD)=SO$.
+) Tìm giao tuyến giữa $(SAB)$ và $(SCD)$.
Trong mặt phẳng $(ABCD)$, gọi $E=AB\cap CD$. Khi đó $$\left. \begin{array}{l} E\in AB\subset (SAB)\\ E\in CD\subset (SCD)\end{array}\right\} \Rightarrow E\in (SAB)\cap (SCD).$$Mặt khác $S\in (SAB)\cap (SCD)$. Vậy $(SAB)\cap (SCD)=SE$.
Trong mặt phẳng $(ABCD)$, gọi $E=AB\cap CD$. Khi đó $$\left. \begin{array}{l} E\in AB\subset (SAB)\\ E\in CD\subset (SCD)\end{array}\right\} \Rightarrow E\in (SAB)\cap (SCD).$$Mặt khác $S\in (SAB)\cap (SCD)$. Vậy $(SAB)\cap (SCD)=SE$.
+) Tìm giao tuyến giữa $(SAD)$ và $(SBC)$.
Trong mặt phẳng $(ABCD)$, gọi $F=AD\cap BC$. Khi đó $$\left. \begin{array}{l} F\in AD\subset (SAD)\\ F\in BC\subset (SBC)\end{array}\right\} \Rightarrow F\in (SAD)\cap (SBC).$$Mặt khác $S\in (SAD)\cap (SBC)$. Vậy $(SAD)\cap (SBC)=SF$.
Trong mặt phẳng $(ABCD)$, gọi $F=AD\cap BC$. Khi đó $$\left. \begin{array}{l} F\in AD\subset (SAD)\\ F\in BC\subset (SBC)\end{array}\right\} \Rightarrow F\in (SAD)\cap (SBC).$$Mặt khác $S\in (SAD)\cap (SBC)$. Vậy $(SAD)\cap (SBC)=SF$.
Ví dụ 2. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Tìm giao tuyến giữa hai mặt phẳng $(SAB)$ và $(SCD)?$
Lời giải.
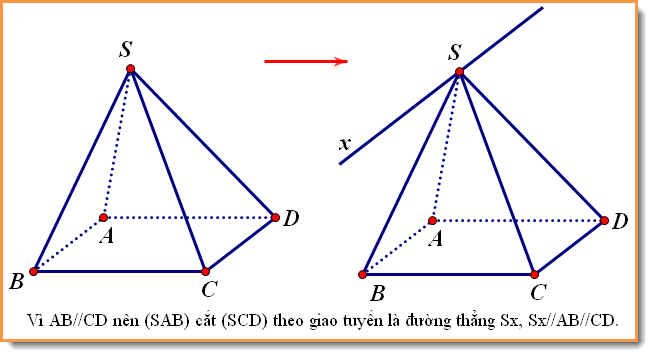
+) Cách 1. Tìm giao tuyến giữa $(SAB)$ và $(SCD)$. (Sử dụng tính chất: Ba mặt phẳng đôi một cắt nhau thì 3 giao tuyến của chúng đồng quy hoặc song song với nhau.)
Ta có $$\left. \begin{array}{l}S\in (SAB)\cap (SCD)\\ (SAB)\cap (ABCD)=AB\\ (SCD)\cap (ABCD)=CD\\ AB//CD\end{array}\right\} \Rightarrow (SAB)\cap (SCD)=Sx, Sx//AB//CD.$$ Vậy $(SAB)\cap (SCD)=Sx, Sx// AB// CD$.
+) Cách 1. Tìm giao tuyến giữa $(SAB)$ và $(SCD)$. (Sử dụng tính chất: Ba mặt phẳng đôi một cắt nhau thì 3 giao tuyến của chúng đồng quy hoặc song song với nhau.)
Ta có $$\left. \begin{array}{l}S\in (SAB)\cap (SCD)\\ (SAB)\cap (ABCD)=AB\\ (SCD)\cap (ABCD)=CD\\ AB//CD\end{array}\right\} \Rightarrow (SAB)\cap (SCD)=Sx, Sx//AB//CD.$$ Vậy $(SAB)\cap (SCD)=Sx, Sx// AB// CD$.
+) Cách 2. Tìm giao tuyến giữa $(SAB)$ và $(SCD)$.
Ta có $$\left. \begin{array}{l}S\in (SAB)\cap (SCD)\\ AB\subset (SAB)\\ CD\subset (SCD)\\ AB//CD\end{array}\right\} \Rightarrow (SAB)\cap (SCD)=Sx, Sx//AB//CD.$$ Vậy $(SAB)\cap (SCD)=Sx, Sx// AB// CD$.
Ta có $$\left. \begin{array}{l}S\in (SAB)\cap (SCD)\\ AB\subset (SAB)\\ CD\subset (SCD)\\ AB//CD\end{array}\right\} \Rightarrow (SAB)\cap (SCD)=Sx, Sx//AB//CD.$$ Vậy $(SAB)\cap (SCD)=Sx, Sx// AB// CD$.
Ví dụ 3. Cho hình chóp $S.ABCD$ và $E$ là một điểm trên cạnh $SC$. Tìm giao tuyến giữa hai mặt phẳng $(SAE)$ và $(SBD)?$
Lời giải.

Phân tích. Hai mặt phẳng $(SAE)$ và $(SBD)$ có điểm chung là $S$. Tuy nhiên ta không tìm thấy mặt phẳng nào chứa cả $AE$ và $BD$, vì 4 điểm $A, B, D, E$ không đồng phẳng. Do đó để tìm điểm chung thứ hai ta tìm cách "mở rộng" mặt phẳng $(SAE)$ thành một mặt phẳng "lớn" hơn sao cho trong mặt phẳng đó có chứa một đường thẳng mà nó có thể cắt được $BD$. Quan sát kỹ hình vẽ ta sẽ thấy mặt phẳng đó là $(SAC)$.
Ta có $S\in (SAE)\cap (SBD)$ và $(SAE)\equiv (SAC)$.
Trong mặt phẳng $(ABCD)$, gọi $F=AC\cap BD$. Khi đó $$\left. \begin{array}{l} F\in AC\subset (SAE)\\ F\in BD\subset (SBD)\end{array}\right\} \Rightarrow F\in (SAE)\cap (SBD).$$ Vậy $(SAC)\cap (SBD)=SF$.

Phân tích. Hai mặt phẳng $(SAE)$ và $(SBD)$ có điểm chung là $S$. Tuy nhiên ta không tìm thấy mặt phẳng nào chứa cả $AE$ và $BD$, vì 4 điểm $A, B, D, E$ không đồng phẳng. Do đó để tìm điểm chung thứ hai ta tìm cách "mở rộng" mặt phẳng $(SAE)$ thành một mặt phẳng "lớn" hơn sao cho trong mặt phẳng đó có chứa một đường thẳng mà nó có thể cắt được $BD$. Quan sát kỹ hình vẽ ta sẽ thấy mặt phẳng đó là $(SAC)$.
Ta có $S\in (SAE)\cap (SBD)$ và $(SAE)\equiv (SAC)$.
Trong mặt phẳng $(ABCD)$, gọi $F=AC\cap BD$. Khi đó $$\left. \begin{array}{l} F\in AC\subset (SAE)\\ F\in BD\subset (SBD)\end{array}\right\} \Rightarrow F\in (SAE)\cap (SBD).$$ Vậy $(SAC)\cap (SBD)=SF$.
Bài tập
Bài 1. Cho hình chóp $SABCD$ có đáy $ABCD$ là hình bình hành tâm $O$. Gọi $M, N, P$ lần lượt là trung điểm của $BC, CD, SO$. Tìm giao tuyến của mặt phẳng $(MNP)$ với các mặt phẳng $(SAB), (SAD), (SBC)$ và $(SCD)$.Bài 2. Cho tứ diện $ABCD$. Gọi $I, J$ lần lượt là trung điểm của $AC$ và $BC$ và $K$ là một điểm trên cạnh $BD$ sao cho $KD< KB$. Tìm giao tuyến của mặt phẳng $(IJK)$ với $(ACD)$ và $(ABD)$.
Bài 3. Cho tứ diện $ABCD$. Gọi $I, J$ lần lượt là trung điểm của $AD$ và $BC$.
a) Tìm giao tuyến của hai mặt phẳng $(IBC)$ và $(JAD)$.
b) Gọi $M$ là một điểm trên cạnh $AB$, $N$ là một điểm trên cạnh $AC$. Tìm giao tuyến của hai mặt phẳng $(IBC)$ và $(DMN)$.
Bài 4. Cho tứ diện $ABCD$ và $M$ là một điểm bên trong tam giác $ABD$, $N$ là một điểm bên trong tam giác $ACD$. Tìm giao tuyến của các cặp mặt phẳng $(AMN)$ và $(BCD)$; $(DMN)$ và $(ABC)$.
Subscribe to:
Post Comments (Atom)







10 comments
Đã add liên kết của bác :^D^:
Hihi, rất vui khi có thêm bạn mới. ^^
hình k gian dễ đc mấy bài đầu.càng về sau nhìn hình càng sợ :d
hinh k gian kho wa :=?
kho that *=*
^^ :D
vv Tớ có một quy luật nhỏ như thế này cho một số bài hình học không gian khi tìm giao tuyến của hai mặt phẳng.
các bạn giải giúp mình bài này với
bài 1. Cho chóp S.ABCD có đáy là hình thang, AD là đáy lớn. Gọi M,N là trung điểm BC,CD. Tìm giao tuyến của
a) (SAC) và (SBD) b) (SMN) và (SAD)
c) (SAB) và (SCD) d) (SMN) và (SAC) e) (SMN) và (SAB)
Còn bí kíp của tớ đây: https://bit.ly/2GWxjCs
Ai giải dùm em bài tập 1 với ạk
Post a Comment
+) Khi đăng nhận xét, bạn vui lòng viết Tiếng Việt đủ dấu và nhận xét đó có liên quan đến bài viết. Rất vui vì bạn đã đọc bài và cho ý kiến.
+) Vì có nhiều spam comments nên chế độ bình luận "ẩn danh" (nặc danh) đã đóng lại.